Data Science

El Data Science o ciencia de datos, ayuda a las empresas a extraer todo el valor de los datos que genera su negocio, para poder tomar decisiones de una manera eficiente utilizando para ello técnicas analíticas.

El concepto de Data Science tiene que ver con todo lo que rodea al Machine Learning -aprendizaje automático- y al Big Data, pero no nos engañemos, por muchas máquinas y algoritmos de Machine Learning para empresas que ya existen y podemos utilizar, si no existe una buen cientifico de datos detrás, el resultado no será el esperado.

El científico de datos o data scientist, es un profesional que sabe de matemáticas -sobre todo de estadística y probabilidad-,  sabe de programación  – R y su némesis Python- y además conoce el negocio de cuyos datos pretende extraer conclusiones y a ser posible hacer predicciones.

En esta entrada voy a explicar algunos conceptos que todo buen data scientist debería dominar a la perfección.

Revisaremos los siguientes conceptos:

R-cuadrado, hipótesis estadísticas, diagramas de dispersión, modelos de regresión, mínimos cuadrados,  p-valor  y test de Chi-cuadrado ${\chi }^2$

 

R-cuadrado $R^2$

Este coeficiente determina la calidad -o bondad- de ajuste de una función o modelo para predecir el valor de una variable -dependiente- en función de una o varias variables independientes.

También podemos definirlo como el porcentaje de variación -por tanto siempre se encuentra entre 0 y 100%- de la variable dependiente, que explica su relación con una o más variables predictoras o independientes. Mientras mayor sea el R-cuadrado, mejor será el ajuste del modelo a sus datos. A R-cuadrado también lo podemos encontrar en la literatura como  «coeficiente de determinación» o determinación múltiple (en la regresión lineal múltiple).

Para entenderlo mejor, veamos una serie de cosas antes.

En estadística, siempre se presupone que dos variables son independientes salvo que se demuestre lo contrario, dos variables -o una variable y un conjunto de otras- no tienen nada que ver entre ellas salvo que que lo probemos.

En estadística llamamos $H_0$ o Hipótesis Teórica, Hipótesis de Partida o hipótesis nula, a aquella hipótesis que dice que las dos variables que quiero estudiar son independientes.

Y vamos a llamar $H_a$ o Hipótesis Alternativa, a aquella hipótesis que dice que las dos variables en estudio están relacionadas (hay una correlación entre ellas).

Generalmente lo que el estadístico quiere probar, es que se cumple la Hipótesis Alternativa, pero como antes he dicho, en estadística se trabaja suponiendo que todas las variables son independientes entre sí, hasta que los datos aporten información que nos diga lo contrario.

La forma de probar la hipótesis alternativa es recogiendo datos y analizandolos gráfica o analíticamente.

En el caso más sencillo, los datos se representa en un eje de coordenadas ($X_1,Y_1$) ,($X_2,Y_2$),…

Al diagrama de puntos resultante se le llama diagrama de dispersión.

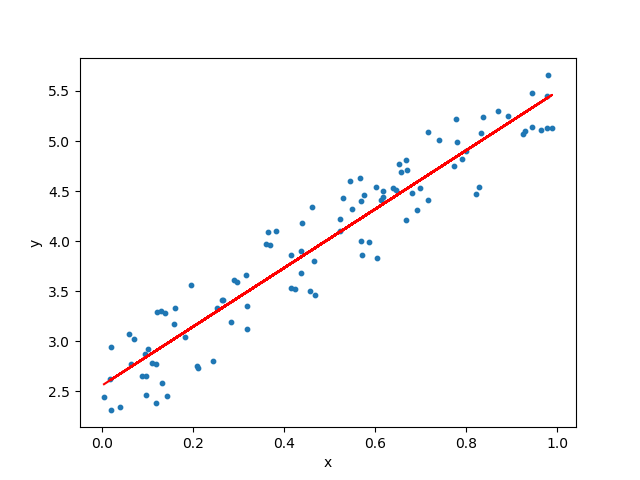
En este ejemplo se ve que hay una tendencia, se observa que a medida que aumentan los valores de la «x», también aumentan los valores de la «y».

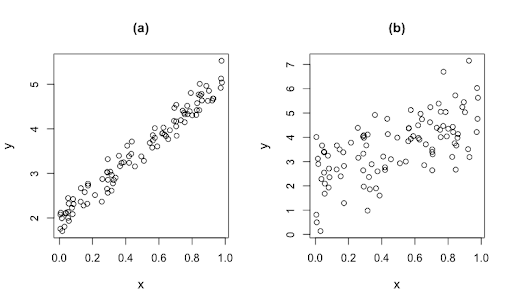
También puede ser como en el caso b) del diagrama anterior en el  que claramente se ve que no hay ninguna relación entre la variable «x» y la variable «y».

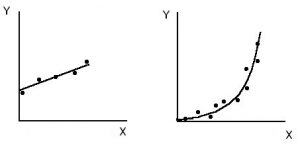
Con el diagrama de dispersión es posible representar una curva que se aproxime a los datos, es decir, que siga la tendencia de los mismos, a esta curva se le llama  curva de aproximación.

La curva de aproximación del primer gráfico tiene pinta de una ecuación lineal, es decir, ecuación de la recta $y=a+bx$; mientras que la del gráfico tiene más pinta de  una ecuación cuadrática -parábola- de la forma $y=a+bx+c{x}^2$.

Al proceso de estimación del valor de una variable en función del valor de otra(s) se le conoce como Regresión.

Si «y» se va a estimar a partir de «x» por medio de alguna ecuación, a esta la llamamos ecuación de regresión de y sobre x  y a la curva correspondiente curva de regresión de y sobre x.

Una forma de determinar si dos variables están relacionadas es calcular el coeficiente de correlación lineal de Pearson que ya expliqué en la entrada de esta web titulada «Estadística y Fondos de Inversión».

$r=\frac{{\sigma }_{xy}}{{\sigma }_x{\sigma }_y}$

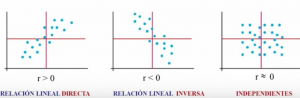
r < 0 Relación lineal inversa

r > 0 Relación lineal directa

r = 0 Un valor 0 -o próximo a 0- de la correlación no quiere decir que dos variables sea independintes. Lo contrario si es cierto, si son independientes la correlación es 0 -podrían ser dependientes pero la relación no ser lineal y la correlación podría ser 0-.

El modelo de regresión lineal simple tiene la forma de la fórmula de una recta en matemáticas.

$y=a+bx$

siendo:

a: El valor que toma la «y» cuando la «x» es cero.

b: La pendiente de la recta (revisar la entrada que escribí sobre derivadas).

Trataremos de buscar una ecuación de la recta que mejor se ajuste a la nube de puntos. Puede haber muchas rectas que se ajusten a la nube de puntos. Para construir las rectas, parábolas u otras curvas de aproximación que mejor se ajusten se suele seguir el Método de Mínimos Cuadrados.

Llamemos $e_i$  al error entre el verdadero valor de $y$ y el valor $\hat{y}$ que es el valor aproximado por nuestra función de regresión.

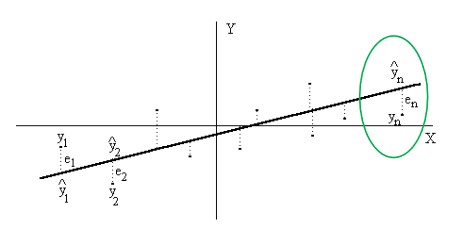
De todas las curvas de aproximación correspondientes a un conjunto de puntos dados, la curva que tenga la propiedad de que $e_1^2+e_2^2+\dots e_n^2$ es mínimo, se conoce como la mejor curva de ajuste.

A estos $e_i$ se les denomina «residuos».

El criterio de mínimos cuadrados requiere la determinación de los valores de “a” y “b”  de la recta tal que el siguiente sumatorio

$\sum _{i=1}^n{e}_i=\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$ sea mínimo.

Es decir, la suma de los cuadrados de las diferencias entre los valores reales observados $y_i$ y los valores estimados ${\hat{y}}_i$ debe ser mínimo.

$\hat{y}=a+bx$

Los valores de a y b de la recta de regresión que aproxima la nube de puntos se obtinenen de la siguiente forma:

a=$\bar{y}–b\bar{x},b=\frac{{\sigma }_{xy}}{{\sigma }_x^2}$

En donde $\bar{x}$ e $\bar{y}$ son las medias de «x» e «y» respectivamente, ${\sigma }_x^2$  es la varianza de «x» y ${\sigma }_{xy}$ es la covarianza entre «x» e «y».

Obtener estos valores se llega a través de unas ecuaciones matemáticas llamadas ecuaciones normales de la recta de regresión de «y» sobre «x» cuya solución son los valores a y b. Aunque «lo que de verdad me pide el cuerpo» es demostrar de donde salen esos valores y que esto no parezca mágia ni dogma de fé, no lo voy a hacer para no distraernos del foco de de llegar a entender R-cuadrado.

Observación: La recta de regresión pasa siempre por el centro de gravedad de la nube de puntos. A «b» se le llama coeficiente de regresión. No confundir con el coeficiente de correlación que es $\frac{{\sigma }_{xy}}{{\sigma }_x{\sigma }_y}$.

Llamamos Error Cuadrático Medio MSE=$\frac{1}{n}\cdot \sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$

El error cuadrático, es preciso, pero algo engañoso, ya que si vemos en una estimación de precios que nuestro sistema tiene un error cuadrático medio de 1 millon de dólares, tenemos que tener presente de que sumamos potencias de 2, en otras palabras sumamos números que previamente hemos elevado al cuadrado. Por lo que el error real, será la raíz cuadrada de ese valor, al cual, por sus siglas en ingés lo denominamos RMSE.

Raíz Cuadrada del Error Cuadrático Medio. MSE=$\sqrt{\frac{1}{n}\cdot \sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2}$

Hasta ahora hemos visto la regresión lineal simple, pero a veces la variable dependiente «y» depende de «n» variables independientes $x_1,x_2,x_3$, …

En este caso, hablamos de regresión lineal múltiple y la función modelo que lo trata de representar tiene la forma:

$\hat{y}=a_1{x}_1+a_2{x}_2+\dots +a_n{x}_n+b$

 

Una vez visto esto, podemos volver a la definición de $R^2$.

El $R^2$ es una medida estadística de qué tan cerca están los datos de la línea de regresión ajustada. También se conoce como coeficiente de determinación, o coeficiente de determinación múltiple si se trata de regresión múltiple. Este oscila entre 0 y 1 -0% y 100%-. Cuanto más cerca de 1 se sitúe su valor, mayor es el ajuste del modelo a la variable que estamos intentando explicar. De forma inversa, cuanto más cerca de cero, menos ajustado estará el modelo y por tanto, menos fiable será.

$R^2=\frac{\text{variación explicada}}{\text{variación real}}$

Varianza del modelo utilizando $\hat{y}$, es decir, la estimación que de «y» hace nuestro modelo entre la varianza de «y».

$R^2=\frac{\sum _{i=1}^n({\hat{y}}_i–\overline{y_i}{)}^2}{\sum _{i=1}^n(y_i-\overline{y_i}{)}^2}$

 

Como ya dije,  $R^2$ siempre está entre 0 y 100%:

• 0% indica que el modelo no explica ninguna porción de la variabilidad de los datos de respuesta en torno a su media.
• 100% indica que el modelo explica toda la variabilidad de los datos de respuesta en torno a su media.

Es importante resaltar que aunque el R-cuadrado nos muestra la bondad de ajuste, no proporciona una prueba de hipótesis formal para esta relación. Un R-cuadrado muy alto no asegura la hipótesis alternativa $H_a$, nos sirve como pista, pero con ello solo no podemos asegurar $H_a$.

El problema del coeficiente de determinación, y por lo cual surge el coeficiente de determinación ajustado, está en que no penaliza la inclusión de variables $x_j$ no significativas. Es decir, si al modelo se añaden «n» variables  que guardan poca relación con «y», $R^2$ aumentará y esto nos confundirá.

El Coeficiente de Determinación Ajustado  penaliza la inclusión de variables, su fórmula es:

${\bar{R}}^2=1-\frac{N-1}{N-k-1}(1–R^2)$

Siendo

N : es el tamaño de la muestra

k: el número de variables explicativas.

A valores más altos de k, más alejado estará el R-cuadrado ajustado del R-cuadrado normal.

 

p-valor

En estadística, un resultado o efecto es estadísticamente significativo cuando es improbable que haya sido debido al azar.

En todo modelo estadístico, el resultado va acompañado de su significación estadística y el p-valor es una medida de significación estadística que podemos definirlo como la probabilidad de error de aceptar la $H_a$ -hipótesis alternativa- como cierta cuando en realidad es falsa. Al ser una probabilidad, varia entre 0 y 1.

Gracias al p-valor sabremos sin nos quedamos con $H_0$ o con $H_a$.

Por decirlo de otra forma, existe una población -todos los datos-, pero yo únicamente tengo una muestra de ellos -mi tabla de datos-,  p-valor me dice la probabiidad de error de que la hipótesis que quiero demostrar se cumpla en mi muestra, pero en realidad luego no se dé en la población.

Si esta probabilidad de error es muy pequeña,  entonces estaremos razonablemente seguros de que se da $H_a$.

Por norma general se suele aceptar un p-valor < 0,05 para rechazar la hipótesis nula de que las variables son independientes y aceptar que las variables están relacionadas. Si p-valor > 0,05 mantenemos la hipótesis teórica de independencia.

Supongamos que tenemos un p-valor =0,09 = 9%  $\Rightarrow$ 9 de cada 100 veces vamos a aceptar la hipótesis alternativa sin ser cierta, 9 de cada 100 veces la muestra que cojamos va a dar por cierta la hipótesis alternativa sin serlo.

¿Cómo decido si me quedo con la hipótesis nula  o con la hipótesis alternativa?

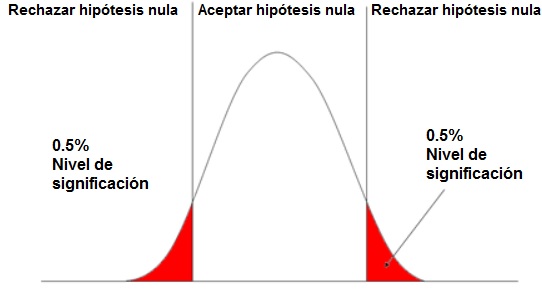
Pues con lo que se llama el nivel de significación o Alpha y normalmente es el 5%

p-valor $>\alpha \Rightarrow$ Me quedo con $H_0$

p-valor $<\alpha \Rightarrow$ Me quedo con $H_a$

El p-valor nos lo suelen calcular todas las herramientas de cálculo estadístico del mercado y por tanto no se suele calcular a mano esta probabilidad.

Ejemplo de una prueba de hipótesis de dos colas con un nivel de significancia $\alpha =1\mathrm{\%}$

 

 

Test Chi-cuadrado de Pearson  ${\chi }^2$

Vamos a estudiar la posible relación entre dos variables cualitativas, es decir, los valores de estas no son numéricos, son categorías.

Vamos a verlo con un ejemplo de una tabla tomada del libro «Bioestadística para las ciencias de la salud», (Martín Andrés, A, Luna Del Castillo, J, 1990). Tenemos la siguiente tabla que recoge información de cuatro tratamientos y tres respuestas diferentes a estos. El tratamiento puede ser cualquiera, por ejemplo una pomada contra la dermatitis.

ixj 4×3	Peor	Igual	Mejor
Tratamiento 1	7	28	115
Tratamiento 2	15	20	85
Tratamiento 3	10	30	90
Tratamiento 4	5	40	115
				560

Tenemos 560 pacientes, según el tratamientos unos han empeorado, otros no han visto ningún cambio y otros han mejorado.

A esta tabla se le llama «tabla de contingencia de dos entradas», por eso en la literatura podemos encontrar esto como el estudio de dos variables cualitativas o como tablas de contingencia –se emplean para analizar la asociación entre dos o más variables cualitativas-.

Estamos hablando de tratamientos médicos, pero esto vale igual para estudiar la opinión sobre partidos políticos y como lo han hecho tras un debate en televisión, o sobre empresas tecnológicas, árboles, etc.

El primer paso siempre es plantearnos:

Hipótesis de Partida $H_0$: Las dos variables que estamos estudiando son independientes.

Hipótesis Alternativa $H_a$: Las dos variable que estamos estudiando están relacionadas.

Si tuviéramos que decantarnos por un tratamiento, obviamente pensaríamos que los buenos -en una primera inspección- son el tratamiento 1 y 4, puesto que en ambos han mejorado 115 pacientes. Pero esto seria si en todos los tratamientos hubiésemos tratado el mismo número de pacientes.

Si sumamos las columnas, vemos que con el tratamiento 1 se han tratado a 150 personas y con el tratamiento 2 han sido tratadas 160. Ya no es lo mismo 115/150 que 115/160

ixj 4×3	Peor	Igual	Mejor
Tratamiento 1	7	28	115	150
Tratamiento 2	15	20	85
Tratamiento 3	10	30	90
Tratamiento 4	5	40	115	160
				560

A esto se le llama calcular las frecuencias marginales de fila.

$f_1=7+28+114=150$ (frecuencia marginal de la primera fila)

$f_4=5+40+115=160$

De igual manera y si lo consideramos interesante, podemos calcular las frecuencias absolutas de columnas, así la frecuencia absoluta de la primera columna es:

$f_{.1}=7+15+10+5=37$ (frecuencia marginal de la primera columna)

ixj 4×3	Peor	Igual	Mejor
Tratamiento 1	7	28	115	150
Tratamiento 2	15	20	85	120
Tratamiento 3	10	30	90	130
Tratamiento 4	5	40	115	160
	37	118	405	560

Pues con esto es con lo que trabajamos, con las frecuencias observadas, con las frecuencias marginales y con el gran total, cuando las variables son cuantitativas, pues trabajamos con las mismas variables calcuando medias, varianzas, etc, pero esto aquí no tiene sentido. No puedo hacer operaciones con el tratamiento 1, 2, 3 y 4, ni con la categoría mejor, peor, etc.

La forma de contrastar $H_0$ es calcular las frecuencias que cabría esperar si las dos variables fueran realmente independientes, la siguiente afirmación sale de un cálculo de probabilidades que aquí no viene al caso demostrar.

$H_0\text{ se cumple }\iff f{e}_{ij}=\frac{(\text{total fila i-ésima})\cdot (\text{total columna j-ésima})}{\text{total global}}$

La frecuencia esperada en la posición ij de la tabla $f{e}_{ij}$ se puede calcular  como

$\frac{(\text{el total de la fila i-ésima})\cdot (\text{el total de la columna j-ésima})}{\text{total global de la tabla}}$

Dibujemos la tabla que contiene las frecuecias observadas y las frecuencias esperadas si las variables fuesen independientes

ixj 4×3	Peor	Igual	Mejor
Tratamiento 1	7 (9,91)	28 (31,61)	115 (108,48)	150
Tratamiento 2	15 (7,93)	20 (25,28)	85 (86,78)	120
Tratamiento 3	10 (8,59)	30 (27,39)	90 (94,02)	130
Tratamiento 4	5 (10,57)	40 (33,72)	115 (115,71)	160
	37	118	405	560

La frecuencia observada $f{o}_{31}=$10

La frecuencia esperada si las dos variables fuesen independientes es $f{e}_{31}=\frac{130\cdot 37}{560}=$8,59

Ahora llega el momento de medir las discrepacias obtenidas, lo cual se hace calculando la diferencia $f{o}_{ij}-f{e}_{ij}$

Pero en lugar de calcular  de esta forma  las discrepancias  para todas las casillas de nuestro ejemplo, las vamos a calcular de la siguiente forma

${\chi }^2=\sum _{ij}^{}\frac{(f{o}_{ij}-f{e}_{ij}{)}^2}{f{e}_{ij}}$

y lo calculamos así porque matemáticamente se ha demostrado que si la Hipótesis de Partida $H_0$ es cierta, ${\chi }^2$ sigue una distribución Chi-cuadrado con (i-1)(j-1) grados de libertad -siendo «i» el número de filas de la tabla y «j» el número de columnas-.

Sabiendo que esto se ajusta a un modelo teórico, asumiendo un nivel de riesgo que estemos dispuestos a asumir, podemos llegar a un punto crítico en el que comparando el ${\chi }^2$ con ese punto crítico podemos decir que:

 

$H_0\text{ es rechazada, i.e. rechazamos la independencia de las variables }\iff {\chi }^2\text{ obtenido/experimental }>{\chi }^2\text{ crítico }$

 

Siendo ${\chi }^2$ crítico un valor obtenido de la tabla de ${\chi }^2$  teórico que vemos más abajo.

En nuestro ejemplo concreto tenemos

${\chi }_{experimental}^2=\frac{(7-9,91{)}^2}{9,91}+\dots +\frac{(115-115,71{)}^2}{115,71}=13,87$

Nos fijamos en la fila de grados de libertad de nuestro caso (i-1)(j-1)=(4-1)(3-1)=6

Nos fijamos en la columna con el riesgo que estemos dispuestos a asumir, generamente se suele aceptar coger un 5%.

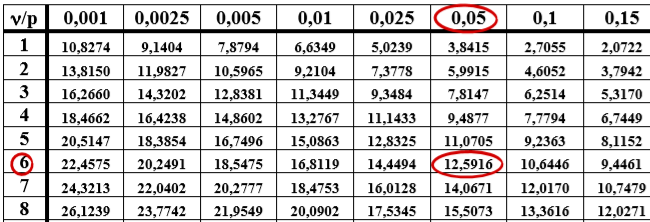
El valor teórico que proporciona el modelo Chi-cuadrado para un error del 5% y un grado de libertad de 6 es 12,5916, i.e.,

${\chi }_{0.05,6}^2=12,5916$

${\chi }_{exp}^2=13,87>125916={\chi }_{0.05,6}^2$

Por lo tantos las variables no son independientes, los resultados (peor, igual, mejor) dependen de los tratamientos.