Las derivadas son muy, pero que muy útiles.
Antes de ver para que sirven las derivadas, vamos a ver qué son las derivadas, y antes de ello, veamos qué es en Matemáticas la pendiente de una recta, ya que así lo vamos a entender todo más fácilmente.
Imaginemos una recta “r” en el eje de coordenadas, definida por los puntos
$$(x_1,y_1) = (6,1) \text{ y } (x_2,y_2) = (10,3)$$
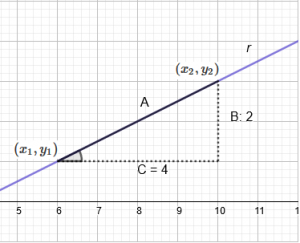
$$\text{La pendiente m de esa recta, en Matemáticas se define como el cociente de } \frac{B}C \text{ y nos marca la inclinación de esa recta.}$$
$$ B=y_2-y_1 \text{ y } C=x_2-x_1.$$
$$\text{m = }\frac{B}C \text{ = } \frac{(y_2-y_1)}{(x_2-x_1)} \text{ = } \frac{2}4 \text{ = 0.5}$$
Si recordamos la trigonometría que nos enseñaron nuestros profesores de mates en el cole, la tangente de un ángulo de un triángulo rectángulo, se define como el cateto opuesto (al ángulo) dividido entre el cateto contiguo (al ángulo),
$$\tan\left(\alpha\right) = \frac{B}C$$
Por lo tanto, la pendiente de una recta también la podemos definir como la tangente del ángulo que forma esa recta con la horizontal (o al cortar el eje de abscisas).
Si el ángulo es de 45 grados, la pendiente m = 1.
La derivada nos sirve para encontrar la pendiente de la recta tangente a una gráfica en un punto x dado.
$$\tan\left(\alpha\right) = m = f'(x)$$
Imaginemos la función siguiente
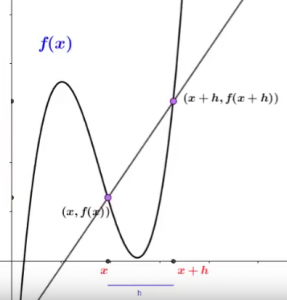
Una forma/truco para obtener la pendiente de la recta tangente a la curva f en el punto (x, f(x)), es imaginarnos una distancia h y obtener otro punto en la curva (x+h, f(x+h)), esto nos da una recta secante a la curva cuya pendiente por lo que vimos al principio sería:
$$m = \frac{y_2-y_1}{x_2-x_1}= \frac{f(x+h)-f(x)}{x+h-x} =\frac{f(x+h)-f(x)}{h}$$
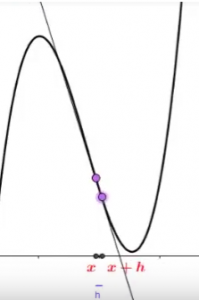
Pero nosotros queremos una recta tangente a la curva en el punto x, no una recta secante, esto lo conseguimos acercándonos mucho con el segundo punto al primero, es decir, cuando el segundo punto esté muy, muy, muy cerca del primero será una recta secante pero que se parecerá mucho a una recta tangente y eso lo podemos solucionar con lo que en matemáticas llamamos límites.
Si hacemos h muy, muy, muy pequeño de forma que h valga 0, ya tendremos la recta tangente porque tocaremos a la gráfica en un único punto y no en dos.
Por lo tanto, la pendiente de la recta tangente en matemáticas lo definimos como
$$m=f’(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$$
Esta fórmula nos daría la pendiente de la recta tangente a la curva en un punto y eso es precisamente a lo que llamamos derivada de una función en un punto, a la pendiente de la recta tangente en ese punto.
Si la relación entre las cantidades x e y viene dada por la fórmula y = f(x), entonces la derivada se indica con una fórmula que representamos como f'(x) -en la notación de Leibniz se escribe $\frac{dy}{dx}$. La fórmula de la derivada nos dice a qué velocidad varía y con respecto a x en cualquier punto x.
El proceso de calcular la función derivada de una función dada se denomina diferenciación y entra dentro del área de las matemáticas denominada cálculo infinitesimal.
Por desengrasar un poco y ver algo práctico, si recordamos lo que era la velocidad, esta se definía como el variación del espacio entre la variación del tiempo, la velocidad expresa la variación de espacio en un incremento de tiempo.
$$v= \frac{\triangle x}{\triangle t}=\frac{x_1-x_0}{t_1-t_0}$$
$$\text{ donde } x_0 \text{ es la posición inicial en el instante inicial } t_0 \text{ y } x_1 \text{ la posicion final}$$
La derivada de una función en un punto mide la velocidad a la que varía el valor de la función en dicho punto al cambiar el valor de la variable independiente X.
La derivada nos da respuesta a preguntas de este estilo:
¿A qué velocidad está cambiando esto? ,¿a qué velocidad estamos conduciendo justo ahora?, ¿a qué velocidad se estará extendiendo la mancha de petróleo del petrolero accidentado al cabo de una semana?
La derivada de la posición de un coche con respecto al tiempo es su velocidad.
Si el eje de abscisas X es el tiempo y el de ordenadas Y el espacio, y a través de una función y=f(x) pintásemos el recorrido que he hecho para ir de un punto a otro, por ejemplo
$$y=2x$$ sería si he ido a una velocidad constante, pero $$y=x^3+3x^2 $$ si a veces he ido más rápido y otras menos.
Por poner un ejemplo sencillo, supongamos que la posición de un coche en una carretera tiene la ecuación $$y=2x$$
Donde y es la posición que varía con el tiempo x. En el origen (x=0) , su posición será y=0
Un segundo después, habrá recorrido 2 metros, dos segundos después 4 metros, etc. La derivada de la posición con respecto al tiempo es la velocidad, entonces el coche va a:
$$v= \frac{\triangle y}{\triangle x}$$ la variación del espacio recorrido con respecto al tiempo, o dicho de otra forma
$$\frac{dy}{dx} = \frac{d2x}{dx}=2m/s$$
Es decir, con las derivadas medimos una magnitud respecto a otra, así como medimos lo rápido que es la variación.
Cálculo de máximos, mínimos y puntos de inflexión.
Las derivadas nos sirven también para obtener los puntos máximos, mínimos y de inflexión de una función.
Máximo relativo
Una función f tiene un máximo relativo en el punto p sí
$$f'(p) = 0$$ y $f´´(p) < 0$
Mínimo relativo
Una función f tiene un mínimo relativo en el punto p sí
$$f'(p) = 0$$ y
$$f´´(p) > 0$$
Punto silla o de inflexión.
Tenemos un punto de inflexión en el punto p cuando:
$$f'(p) =0$$ y
$$f´´(p) = 0$$
Tengamos en cuenta que:
Cuando la derivada de una función es positiva, su pendiente es positiva y por tanto la función es creciente en ese intervalo.
Cuando la derivada de una función es negativa, su pendiente es negativa y por tanto la función es decreciente en ese intervalo.
Por tanto, las derivadas nos sirven para conocer los máximos, mínimos, puntos de inflexión, crecimiento y decrecimiento de funciones polinómicas.
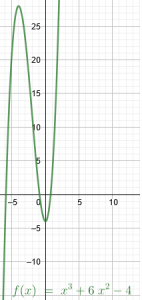
Veámoslo con la función
$$f(x)x^3+6x^2-4$$
$$f'(x)=3x^2+12 $$
Igualamos la derivada a cero y resolvemos la ecuación
$$3x^2+12 = 0 \Rightarrow x^2+4x = 0 \Rightarrow x=\frac{-4 \pm \sqrt{4^2} }{2} $$
Lo cual nos da dos resultados
$$x = -4 \text{ y } x=0$$
$$\text{Tenemos un máximo en } x=-4 \text{ , un mínimo en } x = 0 \text{ y un punto de inflexión en } f’’(x)=0 \Rightarrow 6x+12=0 \Rightarrow x = -2$$
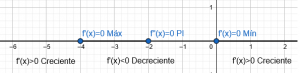
Por ahora ya hemos visto, que las derivadas nos dan información sobre la pendiente de la recta tangente a una curva y además nos informan de cómo cambia una cantidad con respecto a otra. Las derivadas nos indican como cambia puntualmente algo en relación a otro valor que también lo hace, por ejemplo, las variaciones de la temperatura corporal a lo largo del día. Si no cambia nada la temperatura a lo largo del día, entonces diremos que su derivada es cero, porque la temperatura se mantiene constante. La derivada nos da las variaciones que se producen, tanto las que aumentan, tendrían una derivada positiva, como las que disminuyen, tendrían una derivada negativa, es decir nos indican un cambio.
Las derivadas describen los cambios de las funciones y las funciones describen el comportamiento de las cosas. Teniendo esto claro, podemos sacar muchísimos usos de las derivadas.
Imaginemos un fondo de inversión o por ejemplo una empresa que fabrica zapatos sobre la que pudiésemos proponer un modelo matemático (función) que simulase la rentabilidad en el caso del fondo o ganancia en el caso de la empresa, según cuantos zapatos fabricase. Usando derivadas podríamos obtener para la cantidad de zapatos fabricados, la máxima ganancia (sería un punto máximo en su curva/función de nuestro modelo matemático).
También, si fuésemos un arquitecto, sabríamos obtener cuál es el esfuerzo máximo que podríamos ejercer sobre un material. Podríamos poner muchísimos ejemplos.
La derivada de una función nos indica en qué intervalos dicha función es creciente o decreciente. La función puede ser cualquier magnitud dependiente de otra, por ejemplo, el volumen de un gas en función de su temperatura, las ganancias de una empresa en función de su inversión, etc. La derivada, como hemos visto, también sirve para saber para qué valor de la variable independiente la función alcanza un máximo o un mínimo, así que se puede usar para saber cuál es la inversión que maximiza el beneficio de una empresa.
Casi cualquier situación en la que una o varias variables cambien con el tiempo y las causas de dicha variación sean conocidas, la manera de relacionar el efecto con la causa usa derivadas, vamos que las derivadas son muy muy importantes y útiles.
Imaginemos que necesitamos conocer qué factores se han visto afectados en un accidente de tráfico, a veces el pavimento se encuentra en mal estado, puede haber agua o aceite sobre él. Si pretendemos conocer el efecto que tuvo el pavimento, podemos usar derivadas, para plantear ecuaciones del proceso y decidir si la causa fue el agarre. Igualmente con la velocidad inadecuada, etc. A veces en la investigación de un accidente se conoce únicamente la posición final de los vehículos y de manera imprecisa las condiciones previas al accidente. El uso de derivadas y ecuaciones diferenciales es una de las herramientas más usuales.
Si queremos predecir cómo se va a comportar un modelo bajo unas ciertas condiciones, seguro que utilizamos derivadas.
Otros ejemplos de utilización de las derivadas son:
- Igual que la derivada del espacio respecto al tiempo nos da la velocidad, la derivada de la velocidad respecto al tiempo nos da la aceleración.
Recordemos que podemos calcular la aceleración promedio de un objeto en un intervalo de tiempo determinado en base a su velocidad (la rapidez con que viaja en una dirección determinada) antes y después de él. La ecuación de la aceleración: $$a= \frac{\triangle v}{\triangle t}$$ donde a es la aceleración, el numerador es la variación de la velocidad y el denominador es el tiempo en el que ocurre dicha variación. Es decir, la derivada de la velocidad con el tiempo es la aceleración
- La energía potencial es una energía que resulta de la posición o configuración del objeto. Un objeto puede tener la capacidad para realizar trabajo como consecuencia de su posición en un campo gravitacional (energía potencial gravitacional), un campo eléctrico (energía potencial eléctrica), o un campo magnético (energía potencial magnética). La fórmula que lo describe es
$$F=-\frac{dU}{dx}$$La fuerza sobre un objeto, es la negativa de la derivada de la función de potencial U. Esto significa que es la negativa de la pendiente de la curva de energía potencial. Dibujar las curvas de las funciones potenciales, constituyen ayudas valiosas para visualizar el cambio de la fuerza, en una región determinada del espacio.
- La derivada del volumen es el área. Consideremos una esfera, por ejemplo, su volumen se calcula por la fórmula: $$\frac{4}{3}\pi r^3$$ Si la derivamos obtenemos $$4 \pi r^2 $$ que representa la superficie de la esfera. $$\frac{d \text{ volumen de la esfera}}{d \text{ radio de la esfera}} = \text{área de la superficie de la esfera}$$
Para poder comparar corrientes a través de superficies, una magnitud útil es la intensidad de corriente a través de una superficie en un determinado sentido, que se define como la carga que pasa cada unidad de tiempo a través de esa superficie en ese sentido $$i(t)=\frac{dq(t)}{dt}$$
Siendo q(t) la carga que ha atravesado la superficie en el instante t.
Y así podríamos poner infinidad de ejemplos, pero infinidad, las derivadas son importantísimas, así que cuando las estudiamos, tenemos que pensar en lo útiles que son, y no que vamos a memorizar unas fórmulas que apenas sirven para algo. Además, para poder Integrar (que también es muy muy útil) debemos saber primero derivar.
Todos los ejemplos que hemos visto han sido pensando en casos de funciones y=f(x), es decir, funciones con una sola variable independiente, pudiera ser que nos interesase estudiar el comportamiento de una función que depende de dos variables, es decir podemos tener dos variables independientes z=f(x,y) o n variables independientes, aquí entraría en juego el concepto de derivadas parciales de una función que no son el objetivo de esta entrada. Es decir, esto se puede complicar todo lo que queramos, calculando máximos y mínimos de funciones de más dimensiones utilizando derivadas parciales, etc.
Las derivadas para funciones de una variable independiente nos sirven para medir como varia la magnitud de esa función, a partir de cambios que se producen en la variable independiente. Pues las derivadas parciales, nos van a servir para lo mismo, pero para funciones de más de una variable independiente. Imaginemos que tenemos una función f(x,y).
Esta función tiene dos derivadas parciales, la parcial con respecto a x y la parcial con respecto a y,
$$\frac{\partial f}{\partial x} , \frac{\partial f}{\partial y} $$
ya que nosotros podemos analizar como varía el valor de la función a partir de cambios en la variable x manteniéndose y constante (sería la derivada parcial con respecto a x) o podemos estudiar como varía el valor de la función f a partir de cambios en la variable y manteniéndose x constante (sería la derivada parcial con respecto a y).
Esto en la vida real es muy útil si tengo un modelo con varias variables y quiero comprobar cómo se comportaría este si variase una de ellas, por ejemplo contratar un empleado nuevo, si un empleado de una pastelería hace la masa, prepara la nata etc y al día hace 100 pasteles, si modificamos esta “variable” y pasamos a tener dos empleados, haremos 200 pasteles o lo mismo hacemos 220 ya que uno prepara y otro hace (por ejemplo). Esto podría ser un ejemplo para entender el concepto de las derivadas parciales, fijo todas las demás derivadas, muevo solo una de ella y estudio como afecta esto a la función.
Como el mundo está en continuo cambio y las derivadas son el concepto matemático que mejor describe un cambio, por eso digo que las matemáticas están presentes en todas partes.