Con las integrales nos suele pasar lo mismo que con las derivadas, aprendemos a integrar funciones, pero no sabemos realmente cual es la utilidad práctica de todo esto, lo cual hace que se estudien sin motivación.
Cálculo del área
Uno de los mayores problemas del cálculo siempre ha sido la determinación del área comprendida en una región acotada. Una de las soluciones a este problema tiene que ver con la suma de muchos términos.
En matemáticas existe una notación llamada sigma, escrita como la letra griega $\Sigma$ para definir sumas.
La suma de n términos {$x_1, x_2, x_3,… x_n$} se representa así $\sum\limits_{i=1}^n x_i$
Supongamos que queremos calcular el área debajo de esta función:
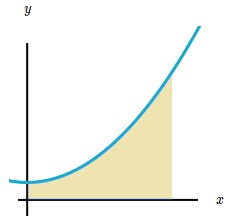
Una forma de hacerlo, es aproximar el área utilizando rectángulos aunque el valor del área no sea (de momento) exacta.
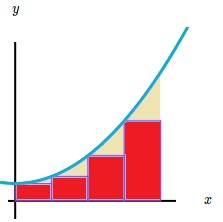
Si hacemos la base de los rectángulos más pequeña, la aproximación es mucho mejor.
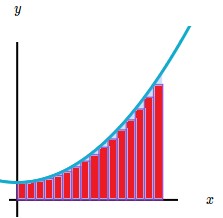
A esta forma de aproximación se le conoce como sumas de Riemann.
Calculando el área de estos rectángulos podemos obtener una aproximación del área buscada.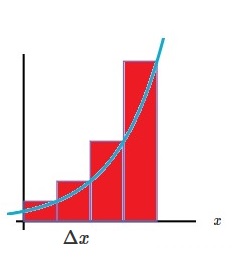
Si los rectángulos están «inscritos», obtenemos una aproximación por defecto y si los rectángulos están circunscritos, obtenemos una aproximación por exceso.
Si la base de los rectángulos (es decir, $\Delta x$) es muy, muy pequeña, la aproximación es cada vez más exacta.
Grosso modo: Si consideramos la base de cada rectángulo ($\Delta x$) y la altura de este, que sería el valor de f(x) para x cualquier punto dentro de la base de cada rectángulo. Sumando las áreas de todos los rectángulos, obtengo una aproximaión del área que hay debajo de la función.
Existe un teorema que dice:
Sea $f$ continua y no negativa en el intervalo [a,b]. El área de la región encerrada por la gráfica $f$, el eje x y las lineas verticales x=a y x=b es:
Área = $\lim\limits_{n\to \infty} \sum\limits_{i=1}^{n} f(c_i)\Delta x_i$ , siendo $x_{i-1} \le c_i \le x_i$ y donde $\Delta x = \frac{(b-a)}{n}$
Claro, cogiendo rectángulos con una base $\Delta x$ infinitesimal, obtenemos el área, es decir, usamos el límite de una suma de áreas de rectángulos para obtener el área de debajo de la función.
Definición de la Integral Definida.
Si f está definida en el intervalo [a, b] y el límite de la suma de Riemann existe, entonces decimos que f es integrable en [a, b] y denotamos este límite mediante
$\lim\limits_{ \Delta x \to 0} \sum\limits_{i=1}^{n} f(c_i)\Delta x_i = \int_a^b f(x)dx$
Llamamos integral definida de f entre a y b a este límite. El número a es el límite inferior de integración y el número b es el límite superior de integración.
Utilizamos dx con el significado de que los$\Delta x$ son muy muy próximos a anchura cero.
El símbolo $\int$ es realmente una «S» muy estilizada con la idea de sumar muchos pedacitos.
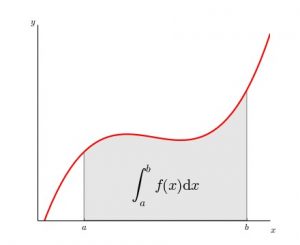
La idea que debemos llevarnos es que cualquier área continua puede ser «troceada» en rectangulitos, en incrementos infinitesimales de modo que la suma del producto de estos anchos (base del rectángulo) por el valor de la función (altura del rectángulo) nos de el área que hay debajo de la función entre dos puntos.
La integral definida de una función entre dos puntos es equivalente al área existente entre la función, el eje de abscisas y las rectas x=a y x=b.
Notemos que con esta definición, una integral definida es un número.
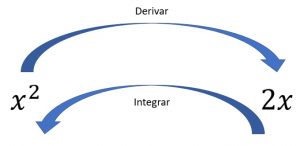
Calcular el limite de un sumatorio nos puede «asustar» un poco, sobre todo si la función no es sencilla. Tranquilos, hay un atajo, y es que calcular una integral es lo contrario a calcular una derivada.
Hasta ahora estamos calculando el área que hay entre una función f, las rectas x=a y x=b y el eje de coordenadas
Pero muy fácilmente se puede deducir el siguiente otro teorema
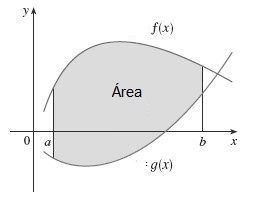
Si dos funciones f y g son continuas en el intervalo [a,b] y $f(x) \ge g(x)$ para todo x en [a,b], entonces el área de la región limitada por las gráficas f, g y las rectas x=a y x=b es
Área =$ \int_a^b [f(x)-g(x)]dx$
En el caso de querer determinar el área entre los puntos de corte de dos funciones, obtendríamos los puntos de corte a y b igualando f(x)=g(x) y luego integraríamos entre esos puntos.
Siempre que podamos calcular algo sumando «trocitos», que al ser más pequeños, pero muchos más, nos sirva para calcular algo, detrás de ello debemos pensar en resolverlo utilizando una integral.
Cálculo del Volumen
Otra aplicación del uso de las integrales es que nos permiten calcular el volumen de sólidos tridimensionales.
Un caso particular de los sólidos tridimensionales son, por ejemplo, los sólidos en revolución que se usan mucho en ingeniería. Llamamos sólido en revolución, al resultado de girar una región del plano alrededor de un eje o línea.
Si giramos un rectángulo alrededor de un eje adyacente a uno de sus lados obtenemos un disco.
El volumen del disco es:
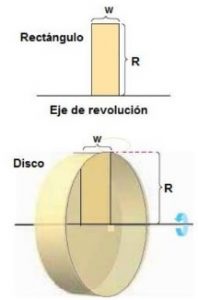
Si una región en el plano gira alrededor de una recta, al sólido resultante se le llama sólido de revolución, y la recta se llama eje de revolución. El sólido de revolución más sencillo es un cilindro o disco que se forma al girar el rectángulo en torno a uno de sus lados.
El volumen de un disco es: Área del disco x Altura del disco =$\pi R^2 w$
Siendo,
R: Radio del cilindro
w: Altura del cilindro
Una vez que hemos aprendido a calcular el volumen de un disco, podemos aproximar el volumen de otras piezas como embudos, pistones de un motor, barricas de vino, etc por aproximación de n discos.
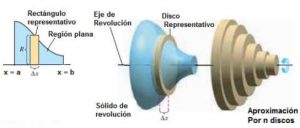
Imaginemos que queremos calcular el volumen de girar la región plana R, alrededor del eje x del primer dibujo anterior.
Podemos aproximar el volumen del sólido por n discos de anchura $\Delta_x$ y de radio $R(x_i)$
El volumen del sólido sería:
Volumen $\approx \sum\limits_{i=1}^{n} \pi [R(x_i)]^2 \Delta x = \pi \sum\limits_{i=1}^{n} [R(x_i)]^2 \Delta x $
Si tomamos límites cuando $\Delta$ tiende a 0 y n a $\infty$
Volumen = $\lim\limits_{ n \to \infty} \pi \sum\limits_{i=1}^{n} [R(x_i)]^2 \Delta x = \pi \int [R(x_i)]^2 dx$
Por decirlo de una forma más genéria, podemos identificar la región plana R, como la el área de una función f sobre el eje x. Es decir, identificar el radio R(x) con la función que vamos a girar f(x) y la anchura del rectángulo $\Delta x$ con dx en la fórmula de la integración.
Trabajo realizado por una fuerza
Decimos que se ha realizado un trabajo cuando una fuerza mueve un objeto, puede ser un coche llevando una carga, comprimir un muelle, etc. Si la fuerza es constante la fórmula de trabajo es la siguiente:
$W = F \cdot D$
siendo W: Trabajo, F: Fuerza constante aplicada, D: Distancia que se ha movido el objeto.
No siempre la fuerza es constante, a veces varia conforme el objeto cambia de posición, por ejemplo en el caso de un coche llevando una carga, el camino tiene cuestas arriba y cuestas abajo, si comprimimos un muelle la fuerza que necesitamos aumenta a medida que vamos comprimiéndolo más y más.
Si comprimimos un muelle, la fuerza que necesitamos aumenta a medida que vamos comprimiéndolo este más y más.
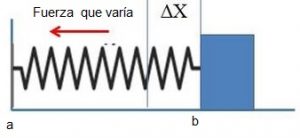
Supongamos que movemos un objeto en línea recta desde x=b hasta x=a debido a una fuerza no constante F(x), una fuerza que va variando. Sea $\Delta x$ una parte del intervalo [a,b] que está divido en n subintervalos.
$a = x_0 < x_1 < x_2 < … < x_n = b$
Sea $\Delta x_i = x_i – x_{i-1}$
Para cada i, elegimos un punto entre medias cualquiera $c_i$ tal que $x_{i-1} \le c_i \le x_i$. En $c_i$ la fuerza viene dada por la función $F(c_i)$, recordemos que la fuerza no es constante, varía continuamente, es decir, $F(c_i)$ cambia.
Si los intervales $\Delta x_i$ son muy pequeños, el trabajo realizado para mover el objeto en el intervalo i-ésimo es aproximado por el incremento $\Delta W_i = F(c_i) \cdot \Delta x_i$ . Siendo W el trabajo cuando la fuerza es constante que hemos visto más arriba.
Sumando el trabajo realizado en cada subintervalo, podemos aproximar el trabajo total que ha realizado el objeto para desplazarse de $a$ hasta $b$ con la siguiente suma:
W $\approx \sum\limits_{i=1}^{n} \Delta W_i = \sum\limits_{i=1}^{n} F(c_i)\Delta x_i$
Esto de sumar trocitos muy pequeños para aproximar el valor de algo mayor ya nos suena de algo y hemos visto que es una integral.
W=$\lim\limits_{ n \to \infty} \sum\limits_{i=1}^{n} F(c_i)\Delta x_i = \int_a^b F(x)dx $
Eureka, resulta que el trabajo realizado por una fuerza variable desde el punto «a» al punto «b» nos lo da la integral definida entre esos puntos.
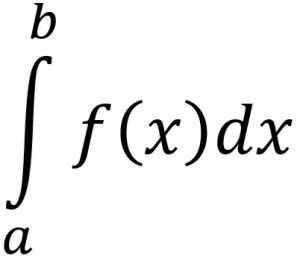
Podríamos ver multitud de ejemplos más acerca del uso de las integrales, como el cálculo de la presión de un fluido, fuerza de un fluido,…

Longitud de arco
El cálculo de la longitud de arco de una curva es un problema también «típico» en matemáticas.
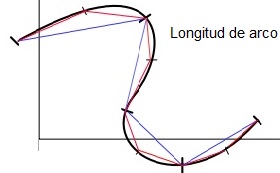
La longitud de este arco podemos verlo como una aproximación de segmentos lineales. Si hay sumas de cosas, en este caso segmentos y que cuanto más pequeños sean estos, más nos aproximamos a longitud del arco que queremos medir, esto ya nos da la «pista» de que nos lo resuelven las benditas integrales.
Existe un teorema que nos lo deja claro:
Si la función y=f(x) tiene una derivada continua f’ en el intervalo [a, b], entonces la longitud de arco de f entre «a» y «b» viene dada por
longitud = $\int_a^b \sqrt{1+[f'(x)]^2} dx$
Espero haber aclarado un poco para qué sirven las integrales y la importancia que estas tienen.