La existencia del número π es conocido desde la antigüedad, pero el cálculo exacto del número no ha sido posible durante siglos.
Veamos tres de los más bellos métodos de calcular el valor del número π
Arquímedes
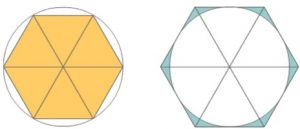 Para calcular el número π, Arquímedes inscribe y circunscribe sendos hexágonos en una circunferencia. Su objetivo es aproximar la longitud de la circunferencia por defecto y por exceso. Si el radio de la circunferencia es r, la longitud de la circunferencia es 2πr. Por otra parte, los perímetros de los hexágonos inscrito y circunscrito son, respectivamente, 6r y 4√3r por lo que
Para calcular el número π, Arquímedes inscribe y circunscribe sendos hexágonos en una circunferencia. Su objetivo es aproximar la longitud de la circunferencia por defecto y por exceso. Si el radio de la circunferencia es r, la longitud de la circunferencia es 2πr. Por otra parte, los perímetros de los hexágonos inscrito y circunscrito son, respectivamente, 6r y 4√3r por lo que
$$ 6r < 2\pi r < 4\sqrt{3}r$$
simplificando dividiendo entre 2r
$$3 < \pi < 2\sqrt{3}=2,4641$$
Finalmente, Arquímedes continúa aumentando el número de lados del polígono regular hasta llegar a los 96 lados obteniendo una aproximación de
$$3,14084507 < \pi < 3,14285714$$
Leibniz
Leibniz descubrió el valor de la serie que lleva su nombre y que es
$$\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{11}-\frac{1}{13}+…$$
Multiplicando ambos lados por 4 obtengo la serie que me da la aproximación del número π.
500.000 números de esta serie nos dan el número π con una precisión de 5 decimales. No es una aproximación muy buena debido al número de términos que hacen falta para alcanzar una aproximación decente, pero la fórmula es preciosa.
Método de Montecarlo
 Un método muy común para estimar el valor de π es mediante el uso de números aleatorios, el método de Montecarlo. En la imagen tenemos un círculo de radio 1, encerrado por un cuadrado de lado 2. El área del círculo es
Un método muy común para estimar el valor de π es mediante el uso de números aleatorios, el método de Montecarlo. En la imagen tenemos un círculo de radio 1, encerrado por un cuadrado de lado 2. El área del círculo es
$$\pi r^2$$
es decir π, y el área del cuadrado será 4. Si dividimos el área del círculo, entre el área del cuadrado obtenemos π/4.
Entonces generamos un gran número de puntos aleatorios uniformemente distribuidos y los representamos en la imagen, esto lo haríamos obteniendo dos coordenadas aleatorias con un ordenador. Estos puntos pueden estar en cualquier posición dentro del cuadrado, pero no tienen por qué caer dentro del círculo. Si caen dentro del círculo, son de color rojo, de lo contrario son de color azul. Si hacemos un seguimiento del número total de puntos N y el número de puntos que están dentro del círculo M y los dividimos, obtenemos un valor aproximado de la relación entre sus áreas, es decir, M/N = π/4, es decir,
$$\pi=4 \cdot \frac{M}{N}$$
Estos son tres de los muchos métodos que hay para calcular el valor de π.
|
Autor |
Época |
Resultado |
|
Arquímedes de Siracusa |
Siglo III AC |
Con un polígono de 96 lados 3,14084507 < π < 3,14285714 |
|
Serie de Leibniz |
Siglos XVII-XVIII |
500.000 números de esta serie nos dan el número π con una precisión de 5 decimales. π=3,14159 |
|
Método Montecarlo |
Siglo XX |
Con 100.000 repeticiones y un ordenador intel i7 se ha obtenido un valor de π= 3,14142 |

