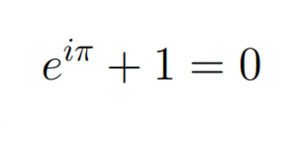En realidad, todos los números son conceptos humanos que modelan la realidad y que han ido apareciendo a medida que el hombre ha ido teniendo necesidades de ellos. Es muy bonita e interesante la histórica de como fueron apareciendo los distintos tipos de números, los naturales positivos, los naturales negativos, el cero, los racionales, los irracionales, los complejos… pero no es el objetivo de esta entrada.
Los números son realmente una invención humana para poder representar la realidad y poder contar, comerciar, etc.
Los números son una abstracción, lo que para nosotros es el símbolo 3 por ejemplo, en China utilizan otro símbolo.
Todos los números son muy interesantes, el tema de los números “no interesantes” lo zanjó el gran Martin Gardner diciendo que si hubiera números no interesantes, los podríamos ordenar en una lista y el primero de esa lista ya tendría una propiedad muy interesante.
En cualquier caso, es cierto que unos son más interesantes que otros, veamos unos cuantos.
- 5040 : Es 7!, además, se puede dividir entre 1,2,3,4,5,6,7,8,9,10, 12, y 49 números más.
En este número se fijó Platón en su libro «El diálogo de las leyes». Platón pensaba que este era el número perfecto de personas a poner en una ciudad porque si tienes que dividir el trabajo entre muchos grupos tienes muchas posibilidades de hacerlo.
- 73: Es el vigésimo primer número primo, $7\times3=21$. 73 leído al revés es el 37 que es el décimo segundo número primo .
- 6174 Constante de Kaprekar.
Elige cualquier número de cuatro cifras. Yo elijo el 1121
Selecciona el número más grande que puedas formar con esas cifras: 2111
Selecciona el número más pequeño que puedas formar con esas cifras: 1112
Réstalos: 2111-1112=999. Si nos diese un número de 3 o menos cifras, lo completaríamos con ceros por delante, en nuestro caso 0999.
Ahora volvemos a hacer los mismo con este número:
9990-0999=8991 y seguimos haciendo lo mismo todo el rato.
9981-1899=8082
8820-0288=8532
8532-2358=6174
Hemos llegado. Siempre se llega a este número. Elijas el número que elijas siempre se llega al 6174, pero es que además es imposible escaparse de el porque si siguiésemos haciendo el mismo procedimiento:
7641-1467=6174
Si llamamos proceso de Kaprekar a elegir un número de «n» cifras, convertirlo en el mayor posible y restarle el menor posible como hemos estado haciendo, 6174 es un punto fijo del proceso de Kaprekar para cuatro cifras.
A los números con esta propiedad se les llama números de Kaprekar.
Para tres cifras el 495 es un punto fijo de Kaprekar. Sólo hay puntos fijos de Kaprekar para números de tres y de cuatro cifras.
- 0: Al principio de las matemáticas no fue considerado un número, porque no servía para contar objetos. Es el primer número natural. Es el valor nulo, por lo que a veces da lugar a indeterminaciones ($\frac{n}{0}\approx\infty$). Marca la frontera entre los números positivos y los negativos y es el único número con la propiedad de que $0=-0$. Tiene características especiales en las potencias.
$ \forall n>0 : n\in\mathbb{R}$, entonces $0^n=0$
$ \forall x\ne0 : n\in\mathbb{R}$, entonces $x^0=1$
$0^0$ es una indeterminación
El 0 junto con el 1 y el infinito podríamos decir que es uno de los tres números protagonistas en el cálculo de límites.
- 1: Es un número muy especial e importante por representar la unidad indivisible en aritmética. Dado cualquier número, creamos el número siguiente añadiendo uno. Es un número realmente especial, $ \forall x\ne0 : n\in\mathbb{R}$ se cumple $1^n=1$. Solo el 0 tiene esta propiedad y además solo él es realmente tan especial como el 1. ¿Crees que el número 1 es primo? No lo es, aunque lo llegó a ser. La definición de número «primo» ha cambiado. Ni es primo ni es compuesto (producto de primos), es especial, es la unidad. Cuando factorizamos un número, sacamos factores primos de un número, esa factorización es única. Por ejemplo:
18 = 3 x 3 x 2 la factorización en números primos es única (aunque cambiemos el orden), si el 1 se considerase primo podríamos decir que 18 = 1 x 3 x 3 x 2 = 1 x 1 x 3 x 3 x 2 = 1 x 1 x 1 x 3 x 3 x 2 es decir, no sería única.
- 2: Es el que «marca» la paridad, el concepto de par o impar, todos los números pares son divisibles por 2. 2 es el único número primo par y además es el primer número primo, ¿verdad que es importante el 2?. Los ordenadores trabajan en binario (potencias de 2), no lo hacen en potencias de 10. 0 es par por ser múltiplo de 2, en concreto 0 x 2
- 3: Es el número primo impar más pequeño. Sólo por ser primo ya es especial, los números primos son como los «ladrillos» de una parte de las matemátias. Cualquier otro número primo es o bien 3k+1 o 3k+2 ($\forall k\in\mathbb{N}$). El espacio que somos capaces de comprender tiene tres dimensiones, bueno, realmente cuatro que son las tres que percibimos más el tiempo, porque el espacio en el que vivimos, según la teoría de cuerdas de nuestros amigos los físicos, tiene en realidad once dimensiones -diez más el tiempo-). Imaginemos un insecto que solo puede ver en 2 dimensiones, si lo dejamos sobre un folio, no podría salirse de él, con lo fácil que sería dar un saltito y salirse del folio, aunque hay más dimensiones el no lo perdibe y no se sale del folio, algo parecido nos pasa a nosotros, pero con tres dimensiones. Esto es el espacio que como humanos somos capaces de comprender, pero por supuesto no para las matemáticas, estas no tienen limitación y «comprenden» la dimensión 4, 5… n, $\forall n\in\mathbb{N}$.
La razón para escoger 11 dimensiones y no otro número, es que 11 es el número que hace que matemáticamente esta estructura funcione sin inconsistencias. Como ya dije en el artículo de esta web titulado «¿Para qué sirven las matemáticas?», estas hacen visible lo invisible.
- Número aureo $\varphi$: Para hablar sobre este número necesitariamos realmente un día entero. El número de oro, la proporción perfecta y divina.
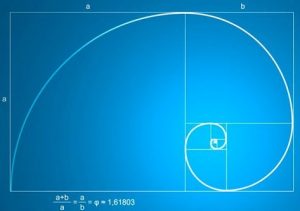
$\frac{a+b}{a} = \frac{a}{b} = \varphi$
$\varphi=\frac{1+\sqrt(5)}{2} = 1,618…$
Este número (esta proporción) se hizo realmente famoso a partir de la publicación del libro del matemático Luca Pacioli «De Divina Proportione» (La Divina Proporción).
- $\pi$: Es sin duda el número más famoso de las matemáticas, encima es una letra en lugar de un número, ¿se le puede pedir más?. Está relacionado con el círculo, pero lo verdaderamente increíble es la facilidad que tiene en aparecer en problemas que nada tiene que ver con la relación entre la longitud de la circunferencia y su radio.
Euler descubrió la fórmula:
$\pi=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}-\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\frac{1}{9}-\frac{1}{10}+\frac{1}{11}+\frac{1}{12}-\frac{1}{13}+…$
(curiosamente en contra de lo que se podría pensar $1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4} + \frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\frac{1}{9} + \frac{1}{10}+\frac{1}{11}+\frac{1}{12} +\frac{1}{13}+…$ no converge a nada.)
También resolvió el Problema de Basilea (suma de los inversos de los cuadrados):
$ \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \frac{1}{5^2} + …=\frac{\pi^2}{6} $
(siempre que la potencia $n$ sea par el límite es de la forma $\frac{\pi^n}{m} $con $m\in\mathbb{Z}$. Si la potencia $n$ es impar, curiosamente el límite no sigue ningún patrón).
Otros matemáticos descubrieron que
$\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{11}-\frac{1}{13}+…$ Serie de Leibniz
$\pi=\frac{2}{\sqrt{2}} \cdot \frac{2}{\sqrt{2+\sqrt{2}}} \cdot \frac{2}{\sqrt{2+\sqrt{2+\sqrt{2}}}} \cdot …$ Vieta
Madhava y Gregory son los descubridores de la siguiente serie infinita para la arctan
$\arctan x = x – \frac{x^3}{3} + \frac{x^5}{5} -\frac {x^7}{7} + \frac{x^9}{9} – …$ haciendo $x = 1$ obtenemos la misma serie de Leibniz.
$\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{11}-\frac{1}{13}+…$
John Wallis descubrió que
$\frac{\pi}{2} = \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdot …$
¿No es increible?, el número $\pi$ aparece cuando menos lo pensamos y sin tener nada que ver con la circunferencia.
$\pi$ no es un número racional, sabemos que es irracional. Llamamos números algebraicos a aquellos que satisfacen una ecuación polinómica con coeficientes enteros. Por ejemplo, $\sqrt{2}$ es algebraico, ya que satisface la ecuación $x^2 – 2 = 0$. Un número que no es algebraico se llama transcendental o transcendente. $\pi$ es transcendente, no es raíz de ninguna ecuación polinómica con coeficientes enteros. ¿Pero que quiere decir realmente que un número es transcendente?, aquellos números irracionales que además son transcendentes, podemos verlos como que son más irracionales que los que no lo son, por ejemplo $\pi$ es más irracional que $\sqrt{2}$
Es decir:
Un número real n es algebraico si existe un polinomio p(x) con coeficientes enteros tal que p(n)=0, es decir, n es raíz de p(x).
Un número real n es trascendente si no es algebraico, es decir, si no existe ningún polinomio con coeficientes enteros tal que alpha sea raíz de él.
Una manera de acordarse de los primeros decimales de pi es contar el número de caracteres de cada palabra en «Sol y luna y cielo proclaman al Divino».
- e : Es un número que representamos por una letra, eso ya le pone al nivel de otros como $\pi$, es transcendente como $\pi$. Es la base de los logaritmos neperianos, lo cual teniendo en cuenta el nombre de esta web es extraordinario. Es irracional y vale 2,718… . Fue descubierto por Jacob Bernoulli (la familia de los Bernoulli fueron grandes matemáticos). Jacob estaba mirando como le resultaba mejor cobrar los intereses de invertir dinero, si cobrar los intereses una vez al año o en más veces y así es como descubrió el número $e$.
Veámoslo con un ejemplo muy sencillo:
Supongamos que el banco nos diera un 100% de interés anual por nuestro dinero.
Si tuviésemos 1€, transcurrido el año tendríamos $\Rightarrow$ 2€.
Jacob pensó, ¿y qué pasaría si pidese cobrar los intereses en dos veces?, una a la mitad del año y otra al finalizar el año, en este caso a la mitad del año tendríamos 1+0,5€ y al final del año otros 0,75€ más, en total 2,25€.
Visto más «matemáticamente», a la mitad del año tenmos $ 1+\frac{1}{2}$ y al final del año habría que sumarle $\frac{1}{2}(1+\frac{1}{2})$ , es decir $1+\frac{1}{2} + \frac{1}{2}(1+\frac{1}{2}) = (1+\frac{1}{2})(1+\frac{1}{2}) = 2,25$
Se puede ver que el patrón es $(1+\frac{1}{2})(1+\frac{1}{2}) $
Como esto tenía muy, pero que muy buena pinta Jacob pensó en ver qué pasaría si decidiese cobrar los interes en tres veces.
Si decidiéramos cobrar los intereses en tres veces, al tercio del año (i.e, a los cuatro meses) tendrímos $1+\frac{1}{3}$, pasan otros cuatro meses y esto se aumenta en otro tercio, es decir$1+\frac{1}{3} + \frac{1}{3}(1+\frac{1}{3})$ y pasan otros cuatro meses y hace el año y eso se ha convertido finalmente siguiendo el patrón en negrita que hemos visto cuando se cobraba en dos partes en $(1+\frac{1}{3})(1+\frac{1}{3})(1+\frac{1}{3}) $= 2,37€.
Es decir, obtendriamos más dinero, ¿y si fuésemos haciendo cada vez intervalos más pequeños, obtendríamos cada vez más y más dinero sin límite?
Si dividimos el año en n intervalos la fórmula general quedaría así:
$(1+\frac{1}{n})^n$
Calculando el límite cuando n tiende a infinito,
$\lim_{n\to \infty} (1+\frac{1}{n})^n=2,7189…=e$
De aquí sale el número e, no obtenemos un interés infinito. e es muy parecido a $\pi$ en el sentido de que «aparece» cuando menos te lo esperas en multitud de sitios y en temas que nada tienen que ver con su origen. Increible, por ejemplo:
$e = \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + … $
Una manera de acordarse de los primeros decimales de pi es contar el número de caracteres de cada palabra en «El trabajo y esfuerzo de recordar e revuelve mi estómago, pero podré acordarme».
- $i$: Es el número imaginario $i=\sqrt-1$, es decir, $i^2=-1$. Da lugar a los números complejos.
Los números han ido apareciendo o el hombre los ha ido creando/descubriendo a medida que los ha ido necesitando. Cuando los matemáticos hemos querido dividir un número entre otro que no daba un resultado exacto, hemos visto la necesidad de inventar/visualizar las fracciones. Cuando hemos querido restar un número grande a otro más pequeño, hemos inventado los números negativos. Cuando algo no lo podemos hacer, los matemáticos inventamos algo que lo resuelva, porque «vemos que está ahí» y solo nos falta definirlo y representarlo. Empezó a ser un problemaen matemáticas que apareciesen raíces cuadradas de números negativos, así que nos inventamos el número i (no sin pocas discusiones, debates, etc).
En el conjunto de los números reales, no existe ningún número que al elevarlo al cuadrado nos de un número negativo. Sin embargo, el número $\sqrt-1$ aparecía muchas veces en matemáticas, lo cual quería decir que algo había que aún no estábamos teniendo en cuenta, así que finalmente se decidió inventar un nuevo conjunto de números, el conjunto de los números complejos. Fue el genial Euler, el que decidió dar el paso y llamar a $i=\sqrt-1$ y lo llamó número imaginario, porque no se comportaba como los número reales conocidos hasta entonces.
Euler descubrió una fórmula maravillosa que engloba a estos números que acabamos de ver incluido el número imaginario i
$e^{i\pi}+1=0$
- 8128: Es un número perfecto.Los griegos hicieron la siguiente clasificación de los números naturales según sus divisores:
Números abundantes: Son aquellos para los cuales la suma de los divisores «propios» (es decir, los divisores excepto el propio número) es mayor que el número.
Números deficientes: Son aquellos para los cuales la suma de los divisores propios es más pequeña que el número.
Números perfectos: Son aquellos para los cuales la suma de los divisores propios es igual al número.
El menor de los números perfecto es 6 ya que 6 = 1 + 2 + 3El siguiente número perfecto es 28 = 1 + 2 + 4 + 7 + 14
- 142857: es lo que se llama un número cíclico y es increíble.
Es la parte periódica de 1/7 =0,142857
Veamos cómo se repiten sus dígitos:
$142 857\cdot 2 = 285714$
$142 857 \cdot3 = 428571$
$142 857 \cdot 4 = 571428$
$142 857 \cdot 5 = 714285$
$142 857 \cdot 6 = 857142$
$142 857 \cdot 7 = 999 999$ Pues sabemos que su origen es de 1/7
$142 857 \cdot 8 = 1 142 856$ El 7 ha desaparecido, pero ha sido sustituido por 1 y 6
$142 857 \cdot 9 = 1 285 713$ perdemos el 4, pero queda 1 y 3
$142 857 \cdot 10 = 1 428 570$
$142 857 \cdot 11 = 1 571 427$ perdemos el 8, pero tenemos un 1 y 7
Continuando todo lo que queramos podemos observar como siguen apareciendo dígitos relacionados.
- 1089: Eligiendo cualquier número de 3 cifras, por ejemplo el 932, poniéndole al revés, 239, lo restamos al primer número por el que hemos empezado 932-239 = 693, le damos la vuelta 396 y lo sumamos al número de antes de darlo la vuelta 396+693 = 1089, siempre obtendremos lo mismo número 1089, curioso.
- 65537: Es un primo de Fermat. Pierre de Fermat pensó que todos los números de la forma $2^{2^n}+1$ eran primos $\forall n\in\mathbb{N}$. Más tarde Euler demostró que no era así. Todos los números primos que son de esta forma dan lugar a polígonos que se pueden pintar con regla sin marcar y un compás. A todos los primos que son de esta forma se les llama primos de Fermat.
- 220 y 184 son números amigos. En matemáticas se llaman números amigos a aquellos números que cumplen que la suma de los divisores de un número da el otro número y viceversa.
- $4^2, 34^2$. ¡Qué curioso!. Tomemos el cuadrado de 4 y el cuadrado de 34
$4^2=16$
$34^2=1156$
observamos algo curioso: para pasar de 16 a 1156 basta colocar el 15 entre los dígitos de 16. Volvamos a colocar 15 en medio de 1156, obtenemos 111.556 que es el cuadrado de 334. Resulta que
$4^2=16$
$34^2=1156$
$334^2=111556$
$3334^2=11115556$
.
.
.
- Pirámide bella
1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321
Para finalizar y como curiosidad indicar cuales eran los números para los griegos, letras que tanto nos gusta usar a los matemáticos:
| 1 | $\alpha$ | alpha | 10 | $\iota$ | iota | 100 | $\rho$ | rho |
| 2 | $\beta$ | beta | 20 | $\kappa$ | kappa | 200 | $\sigma$ | sigma |
| 3 | $\gamma$ | gamma | 30 | $\lambda$ | lambda | 300 | $\tau$ | tau |
| 4 | $\delta$ | delta | 40 | $\mu$ | mu | 400 | $\upsilon$ | upsilon |
| 5 | $\epsilon$ | epsilon | 50 | $\nu$ | nu | 500 | $\phi$ | phi |
| 6 | vau | 60 | $\xi$ | xi | 600 | $\chi$ | chi | |
| 7 | $\zeta$ | zeta | 70 | $\omicron$ | omicron | 700 | $\psi$ | psi |
| 8 | $\eta$ | eta | 80 | $\pi$ | pi | 800 | $\omega$ | omega |
| 9 | $\theta$ | theta | 90 | koppa | 900 | sampri |
Así sumaban los griegos:
32+7=39
$\lambda\beta + \zeta=\lambda\theta$
320+50 = 370
$\tau\kappa + \nu = \tau\omicron$
Juanjo Bravo